按比例绘制的图形 - 彭博社
bloomberg
 摄影:David Elfstrom/Getty Images 这个提高你SAT分数的建议是由Samhita Noone提供的,来自Veritas Prep。
摄影:David Elfstrom/Getty Images 这个提高你SAT分数的建议是由Samhita Noone提供的,来自Veritas Prep。
SAT数学中的大多数图形都是按比例绘制的,你应该利用这一点。学生们常常忽视这样一个事实:如果问题没有在图形的下方或上方注明“图形未按比例绘制”,那么图形就是准确绘制的,这意味着你可以自由估算。你不必为每一个问题都明确计算。
什么时候应该估算?如果你能计算出数字,那就去做。在许多问题中,答案选项会过于相似,以至于估算无法提供有意义的排除方法。估算将允许你确认你的答案选择,并确保你没有在算术上犯错。此外,通常有几个选项是明显的异常值,估算可以让你排除这些选项。从统计上讲,如果你能排除一个答案选项,你应该去猜测。
基本上,如果你对如何解决一个问题毫无头绪,而这个问题附带一个按比例绘制的图形,那么就去检查一下你是否能排除一个答案,然后猜测。即使你已经计算过数字,也要快速检查图形,以确保你的答案是合理的。
让我们来看一个示例问题,看看我们如何练习这个策略。以下内容出现在2013-14年官方大学委员会预试中。首先,我会计算数字。其次,我会通过估算来解决问题。
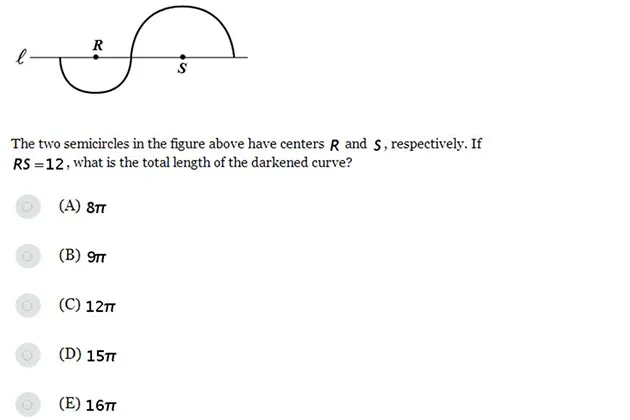
方法 1 这个问题中的关键字是“半圆”,它被定义为正好是一个圆的一半。你可能不知道该如何处理那个奇怪的曲线,但你确实有公式来处理圆。知道这一点后,你可以将 RS 分解为半圆的两个半径。如果我将直线 l 和曲线的交点标记为 X,我可以说 RS = RX + XS。由于 RS = 12,我们知道 RX + XS = 12。
接下来,我要考虑我实际上想要解决的问题。我需要曲线的长度(我将称之为 C),这意味着我需要第一个圆的周长的一半加上第二个圆的周长的一半。周长的公式是 2πr。我可以将 RS 和 XS 作为这个公式中的半径(r),因为问题告诉我们点 R 和 S 位于半圆的中间。
因此 C = 1/2 2πRX + 1/2 2πXS。
我可以简化为 C = πRX + πXS 然后我可以将 π 从两个项中提取出来:C = π(RX + XS)
最后,我们已经知道 RX + XS = 12。我们可以将其代入,最终得到:C = 12π。 答案是 C。
方法 2 让我们忘掉所有那些方程。这个图是按比例绘制的,所以我将大致标记它。仅仅通过目测,RX 看起来大约是 RS 的三分之一。由于 RS = 12,我只是估计 RS = 4。然后我尝试将曲线分成 RX 大小的部分,结果我得到了稍微多于 9 个这样的部分。9×4 = 36,所以我将猜测曲线稍微大于 36 个单位。最接近的答案是 C。
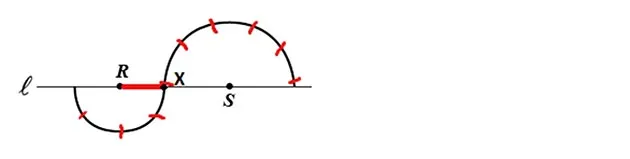
即使我的估计有些偏差,我仍然可以轻松排除选项D和E;这两个选项与36有很大不同。到那时,我是在三种选项中猜测,如果你能排除一个选项,猜测对你是有利的。
最近宣布将对SAT进行重大更改。要全面了解即将到来的SAT更改,请点击 这里。