SAT几何：潜伏的梯形，隐藏的三角形 - 彭博社

照片由 Radius Images/Corbis 提供 这个提高你 SAT 分数的建议是由 Veritas Prep 提供的。

欧几里得几何和坐标几何都是你在 SAT 中需要熟悉的科目，以便获得好成绩。总会有十几个问题与几何概念相关。虽然三角学不是 SAT 的官方主题，但你确实需要知道如何以及何时在某些问题中应用毕达哥拉斯定理。不过不用担心：你不需要记住公式，因为每个 SAT 数学部分的开头都会提供一个公式表。

我们想强调的是，SAT 不仅仅是将数字代入公式并得出答案；它需要你运用推理能力来判断何时适合和有用地应用毕达哥拉斯定理。此外，有时甚至不明显你可以应用公式来帮助你解决问题。你需要在问题中寻找“隐藏的三角形”来帮助你找到解决方案。一旦你知道要寻找什么，你会开始在各处看到隐藏的直角三角形，并能够利用它们来帮助你解决困难的几何 SAT 问题。

让我们来看一下 2007-2008 年官方 SAT 练习测试中出现的以下问题：

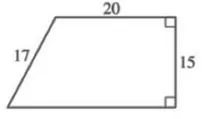
上面的梯形的周长是多少？ A) 52 B) 72 C) 75 D) 80 E) 87

你还记得在这种情况下计算梯形周长的公式吗？你不记得？没关系，因为没有一个公式。那么我们应该如何解决这个问题呢？这就是“隐藏三角形”概念发挥作用的地方。这里的问题是我们不知道梯形底边的长度，所以我们需要稍微创造性地解决它。仔细看看，我们可以从梯形的顶部画一条直线到底边，形成一个三角形，如下所示：

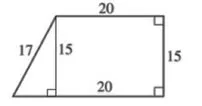
这就是我们的隐藏三角形。现在我们有一个底边为20，边长为15的矩形，附加在一个直角三角形上。如果我们能找出左侧三角形的底边，我们就会拥有计算整个形状周长所需的所有组件。让我们应用我们的勾股定理，其中17是斜边，15是其中一条边，我们让x为剩余的边：

172 = 152 + x2 289 = 225 + x2 64 = x2 x = 8

现在我们知道三角形的底边是20 + 8 = 28。让我们将其他边相加：28 + 17 + 15 + 20 = 80，或者选择D。

你看到隐藏三角形如何帮助我们解决这个几何问题了吗？下次遇到SAT几何问题时要寻找它们。

如果你对这个问题感到完全困惑，你也可以使用你的SAT考试准备策略来排除一些错误的答案选择。我们知道前三条边的总和是52（17 + 20 + 15）。我们还知道梯形的底边必须大于顶部或大于20。因此，我们知道周长大于72。这使我们能够排除一些太小的答案选择：

A) 52 B) 72 C) 75 D) 80 E) 87

此外，你可能可以安全地排除答案选择C，因为它的值太小，以及答案选择E，因为它的值太大，基于图形其余部分的相对长度。无论如何，你在这个问题上获得了优势，即使无法达到完整的解决方案，你也会处于良好的猜测区域。一些聪明的排除策略在SAT考试中可以值几个分数。

即将参加SAT考试？注册试用 Veritas Prep SAT 2400按需课程。