GMAT提示：几何问题真正测量的内容 - 彭博社

bloomberg

2013-08-01

摄影由Getty Images提供 这个提高GMAT分数的建议是由Brian Galvin提供的，来自 Veritas Prep。

你上次在工作中使用毕达哥拉斯定理是什么时候？除非你是数学老师或金字塔建筑师，否则答案很可能是“从未”。那么，GMAT为什么要测试几何呢？

虽然这个常见的问题可能看起来像是那些厌恶空间思维或三的平方根的人的酸葡萄心理，但实际上这是一个有意义的练习，旨在调整你的心态，以便在基于几何的问题上取得成功。GMAT并不是因为几何公式在商学院中本质上有用而测试几何；它测试几何是因为它非常适合评估与商业相关的问题解决能力。

简单来说，商业就是利用资产，而几何问题也是如此。

考虑以下例子：

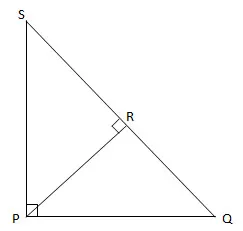
在三角形PQS中，如果PQ = 3且PS = 4，则PR =

(A) 9/4 (B) 12/5 (C) 16/5 (D) 15/4 (E) 20/3

当许多人尝试回答这个问题时，他们的第一反应是假设线SR和RQ是相等的——即线PR平分边SQ。但事实并非如此。PQ和PS的长度不同这一事实应该告诉你，三角形并不对称，因此线PR不会简单地将其一分为二。接下来，更痛苦的反应是试图深入进行复杂的毕达哥拉斯定理计算，这通常会导致大量的挫败感。

但这里是GMAT几何的解决问题/利用资产的特性可以帮助你的地方。快速解决这个问题的关键实际上是你对三角形最基本的知识之一：

面积 = ½ 底边 X 高度。

为什么？因为如果你把PQ作为大三角形的底边，那么PS就是高度（底边和高度必须垂直），这意味着面积是½(3)(4) = 6。但然后在脑海中将那个三角形翻转，使其位于SQ边上，并使用SQ作为底边。那么，哪条线是高度？PR线，即底边与对角线之间的垂直线。既然你知道SQ = 5（你可以通过毕达哥拉斯定理得到这个）并且面积是6，你现在有：

面积 = ½ 底边 X 高度

6 = ½ (5)(h)

h = 12/5

虽然这个问题的机制确实要求你知道毕达哥拉斯定理和三角形的面积，但你应该看到这个问题更多的是关于创造性地利用资产（很少有人将面积视为资产），而不仅仅是纯粹的几何。

商业会奖励你找到高效和独特的方式将资产结合在一起，而GMAT几何在很大程度上也是如此。学习几何以建立你的资产库，但请记住，你这样做的原因是专注于创造性应用——你想向商学院展示的真正资产。